ADAPT VQE¶
Overview¶
In this notebook, we will implement ADAPT-VQE, to show how to use TenCirChem to build novel algorithms.
Form Operator Pool¶
[1]:
from tencirchem import UCC
from tencirchem.molecule import h4
ucc = UCC(h4)
# get single and double excitations
# param_id maps operators to parameters (some operators share the same parameter)
ex1_ops, ex1_param_ids, _ = ucc.get_ex1_ops()
ex2_ops, ex2_param_ids, _ = ucc.get_ex2_ops()
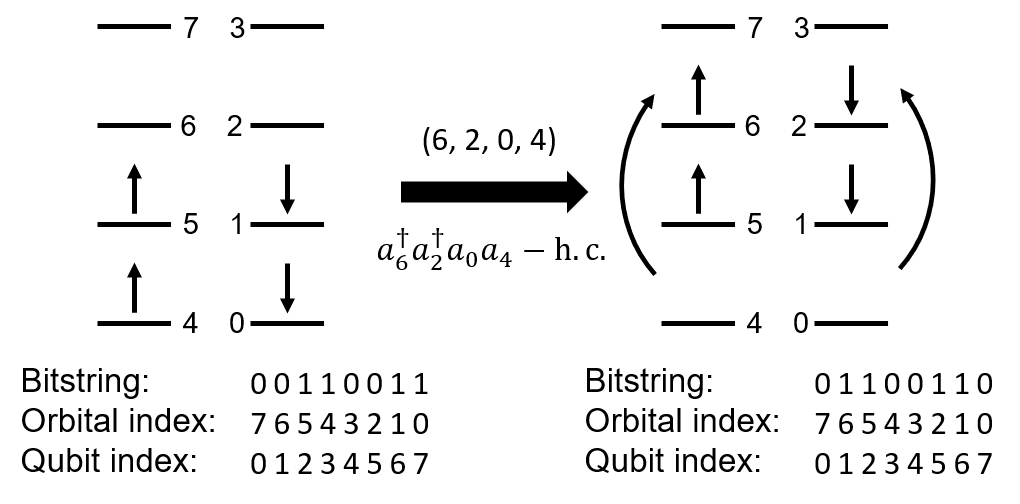
The meanings of the numbers are best summarized in the following figure. The elements in the tuples are spin-orbital indices, with the first half and the second half corresponds to creation and annihilation operators, respectively.
[2]:
list(zip(ex1_ops, ex1_param_ids))
[2]:
[((6, 4), 0),
((2, 0), 0),
((7, 4), 1),
((3, 0), 1),
((6, 5), 2),
((2, 1), 2),
((7, 5), 3),
((3, 1), 3)]
[3]:
list(zip(ex2_ops, ex2_param_ids))
[3]:
[((6, 7, 5, 4), 0),
((2, 3, 1, 0), 0),
((2, 6, 4, 0), 1),
((2, 7, 4, 0), 2),
((6, 3, 0, 4), 2),
((3, 7, 4, 0), 3),
((2, 6, 5, 0), 4),
((6, 2, 1, 4), 4),
((2, 7, 5, 0), 5),
((6, 3, 1, 4), 5),
((3, 6, 5, 0), 6),
((7, 2, 1, 4), 6),
((3, 7, 5, 0), 7),
((7, 3, 1, 4), 7),
((2, 6, 5, 1), 8),
((2, 7, 5, 1), 9),
((6, 3, 1, 5), 9),
((3, 7, 5, 1), 10)]
[4]:
# group the operators to form an operator pool
# operators with the same parameter are grouped together.
from collections import defaultdict
op_pool = defaultdict(list)
for ex1_op, ex1_id in zip(ex1_ops, ex1_param_ids):
op_pool[(1, ex1_id)].append(ex1_op)
for ex2_op, ex2_id in zip(ex2_ops, ex2_param_ids):
op_pool[(2, ex2_id)].append(ex2_op)
op_pool = list(op_pool.values())
op_pool
[4]:
[[(6, 4), (2, 0)],
[(7, 4), (3, 0)],
[(6, 5), (2, 1)],
[(7, 5), (3, 1)],
[(6, 7, 5, 4), (2, 3, 1, 0)],
[(2, 6, 4, 0)],
[(2, 7, 4, 0), (6, 3, 0, 4)],
[(3, 7, 4, 0)],
[(2, 6, 5, 0), (6, 2, 1, 4)],
[(2, 7, 5, 0), (6, 3, 1, 4)],
[(3, 6, 5, 0), (7, 2, 1, 4)],
[(3, 7, 5, 0), (7, 3, 1, 4)],
[(2, 6, 5, 1)],
[(2, 7, 5, 1), (6, 3, 1, 5)],
[(3, 7, 5, 1)]]
ADAPT-VQE Iteration¶
Once the operator pool is formed, ADAPT-VQE constructs the ansatz by picking operators in the pool iteratively. The criteria for picking the operators is to maximize the absolute energy gradient if the operator is picked. Supposing the original ansatz wavefunction is \(| \psi \rangle\) and the operator picked is \(G_k\), the new ansatz with \(G_k\) is
\[| \Psi \rangle = e^{\theta_k G_k} | \psi \rangle \ ,\]
and the energy gradient is
\[\frac{\partial \langle E \rangle }{\partial \theta_k} =2 \langle \Psi|HG_k|\Psi \rangle \ .\]
With \(\theta_k = 0\), the gradient is then
\[\frac{\partial \langle E \rangle }{\partial \theta_k}\bigg{|}_{\theta_k=0} = 2 \langle \psi|HG_k|\psi \rangle \ .\]
If multiple operators sharing the same parameter are added at the same time, then their gradient should be added together. The iteration stops when the norm of the gradient vector is below a predefined threshold \(\epsilon\). In the following, \(| \psi \rangle\) is obtained by ucc.civector() as a vector in the configuration interaction space.
[5]:
import numpy as np
ucc.ex_ops = []
ucc.params = []
ucc.param_ids = []
converged = False
MAX_ITER = 100
EPSILON = 1e-3
for i in range(MAX_ITER):
print(f"######## Iter {i} ########")
# calculate gradient of each operator from the pool
op_gradient_list = []
psi = ucc.civector()
bra = ucc.hamiltonian(psi)
for op_list in op_pool:
grad = bra.conj() @ ucc.apply_excitation(psi, op_list[0])
if len(op_list) == 2:
grad += bra.conj() @ ucc.apply_excitation(psi, op_list[1])
op_gradient_list.append(2 * grad)
print("Gradient vector norm: ", np.linalg.norm(op_gradient_list))
print("Nonzero gradient vector elements:")
for op_list, g in zip(op_pool, op_gradient_list):
if np.abs(g) < 1e-10:
continue
print(f"{g:.10f}", op_list)
if np.linalg.norm(op_gradient_list) < EPSILON:
print(f"Converged. Norm of gradient: {np.linalg.norm(op_gradient_list)}")
break
chosen_op_list = op_pool[np.argmax(np.abs(op_gradient_list))]
print("Picked operator", chosen_op_list)
if ucc.ex_ops[-len(chosen_op_list) :] == chosen_op_list:
print(f"Converged. Same operator picked in succession")
break
# update ansatz and run calculation
ucc.ex_ops.extend(chosen_op_list)
ucc.params = list(ucc.params) + [0]
ucc.param_ids.extend([len(ucc.params) - 1] * len(chosen_op_list))
ucc.init_guess = ucc.params
ucc.kernel()
print(f"Optimized energy: {ucc.e_ucc}")
else:
print("Maximum number of iteration reached")
######## Iter 0 ########
Gradient vector norm: 0.6413625239691856
Nonzero gradient vector elements:
0.0000001787 [(6, 4), (2, 0)]
-0.0000001938 [(7, 5), (3, 1)]
0.2103420256 [(6, 7, 5, 4), (2, 3, 1, 0)]
0.2141378225 [(2, 6, 4, 0)]
0.1874444822 [(3, 7, 4, 0)]
0.3756623781 [(2, 7, 5, 0), (6, 3, 1, 4)]
0.1653203524 [(3, 6, 5, 0), (7, 2, 1, 4)]
0.2765500090 [(2, 6, 5, 1)]
0.2029254292 [(3, 7, 5, 1)]
Picked operator [(2, 7, 5, 0), (6, 3, 1, 4)]
Optimized energy: -2.130032459500918
######## Iter 1 ########
Gradient vector norm: 0.5218024526621244
Nonzero gradient vector elements:
-0.0125038973 [(6, 4), (2, 0)]
0.0167842115 [(7, 5), (3, 1)]
0.1713002616 [(6, 7, 5, 4), (2, 3, 1, 0)]
0.2226765539 [(2, 6, 4, 0)]
0.2132785933 [(3, 7, 4, 0)]
0.1071344471 [(3, 6, 5, 0), (7, 2, 1, 4)]
0.3020073191 [(2, 6, 5, 1)]
0.2115115746 [(3, 7, 5, 1)]
Picked operator [(2, 6, 5, 1)]
Optimized energy: -2.1521053433859345
######## Iter 2 ########
Gradient vector norm: 0.4071773446367265
Nonzero gradient vector elements:
0.0401782688 [(6, 4), (2, 0)]
-0.0344678940 [(7, 5), (3, 1)]
0.1829807723 [(6, 7, 5, 4), (2, 3, 1, 0)]
0.1754330302 [(2, 6, 4, 0)]
0.2209264766 [(3, 7, 4, 0)]
0.0035378050 [(2, 7, 5, 0), (6, 3, 1, 4)]
0.1519036061 [(3, 6, 5, 0), (7, 2, 1, 4)]
0.1638188641 [(3, 7, 5, 1)]
Picked operator [(3, 7, 4, 0)]
Optimized energy: -2.1560078326527474
######## Iter 3 ########
Gradient vector norm: 0.3397631170243717
Nonzero gradient vector elements:
0.0447472512 [(6, 4), (2, 0)]
-0.0390906463 [(7, 5), (3, 1)]
0.1863194802 [(6, 7, 5, 4), (2, 3, 1, 0)]
0.1647591097 [(2, 6, 4, 0)]
0.0000000382 [(3, 7, 4, 0)]
-0.0000000803 [(2, 7, 5, 0), (6, 3, 1, 4)]
0.1629033819 [(3, 6, 5, 0), (7, 2, 1, 4)]
-0.0000000722 [(2, 6, 5, 1)]
0.1533315226 [(3, 7, 5, 1)]
Picked operator [(6, 7, 5, 4), (2, 3, 1, 0)]
Optimized energy: -2.158313503086184
######## Iter 4 ########
Gradient vector norm: 0.2904720974252725
Nonzero gradient vector elements:
0.0507437926 [(6, 4), (2, 0)]
-0.0431791207 [(7, 5), (3, 1)]
-0.0000000009 [(6, 7, 5, 4), (2, 3, 1, 0)]
0.1548519273 [(2, 6, 4, 0)]
0.0000000012 [(3, 7, 4, 0)]
-0.0000000017 [(2, 7, 5, 0), (6, 3, 1, 4)]
0.1881028425 [(3, 6, 5, 0), (7, 2, 1, 4)]
0.0000000006 [(2, 6, 5, 1)]
0.1434324638 [(3, 7, 5, 1)]
Picked operator [(3, 6, 5, 0), (7, 2, 1, 4)]
Optimized energy: -2.160631774640665
######## Iter 5 ########
Gradient vector norm: 0.23155645245221745
Nonzero gradient vector elements:
0.0418683900 [(6, 4), (2, 0)]
-0.0344273185 [(7, 5), (3, 1)]
0.1647882822 [(2, 6, 4, 0)]
-0.0000000002 [(3, 7, 4, 0)]
0.1533786504 [(3, 7, 5, 1)]
Picked operator [(2, 6, 4, 0)]
Optimized energy: -2.164921018130742
######## Iter 6 ########
Gradient vector norm: 0.16766398932285673
Nonzero gradient vector elements:
0.0241699861 [(6, 4), (2, 0)]
-0.0308084251 [(7, 5), (3, 1)]
0.0004344058 [(6, 7, 5, 4), (2, 3, 1, 0)]
0.0012217449 [(3, 7, 4, 0)]
0.0008976241 [(2, 7, 5, 0), (6, 3, 1, 4)]
0.0004632254 [(3, 6, 5, 0), (7, 2, 1, 4)]
0.0003003856 [(2, 6, 5, 1)]
0.1630186312 [(3, 7, 5, 1)]
Picked operator [(3, 7, 5, 1)]
Optimized energy: -2.1674443274948185
######## Iter 7 ########
Gradient vector norm: 0.026968274543560385
Nonzero gradient vector elements:
0.0206092184 [(6, 4), (2, 0)]
-0.0173939056 [(7, 5), (3, 1)]
-0.0000000813 [(6, 7, 5, 4), (2, 3, 1, 0)]
0.0000000039 [(2, 6, 4, 0)]
0.0000001792 [(3, 7, 4, 0)]
0.0000001301 [(2, 7, 5, 0), (6, 3, 1, 4)]
-0.0000000779 [(3, 6, 5, 0), (7, 2, 1, 4)]
-0.0000000055 [(2, 6, 5, 1)]
0.0000000310 [(3, 7, 5, 1)]
Picked operator [(6, 4), (2, 0)]
Optimized energy: -2.1674988485893616
######## Iter 8 ########
Gradient vector norm: 0.022742856617093358
Nonzero gradient vector elements:
-0.0000000004 [(6, 4), (2, 0)]
-0.0227422801 [(7, 5), (3, 1)]
0.0001099764 [(6, 7, 5, 4), (2, 3, 1, 0)]
0.0000004105 [(2, 6, 4, 0)]
0.0000167703 [(3, 7, 4, 0)]
0.0001173127 [(2, 7, 5, 0), (6, 3, 1, 4)]
0.0000073356 [(3, 6, 5, 0), (7, 2, 1, 4)]
0.0000055027 [(2, 6, 5, 1)]
Picked operator [(7, 5), (3, 1)]
Optimized energy: -2.1675452943964704
######## Iter 9 ########
Gradient vector norm: 2.482330523964407e-05
Nonzero gradient vector elements:
-0.0000000015 [(6, 4), (2, 0)]
-0.0000000041 [(7, 5), (3, 1)]
-0.0000059866 [(6, 7, 5, 4), (2, 3, 1, 0)]
-0.0000001058 [(2, 6, 4, 0)]
0.0000190189 [(3, 7, 4, 0)]
0.0000015227 [(2, 7, 5, 0), (6, 3, 1, 4)]
0.0000075106 [(3, 6, 5, 0), (7, 2, 1, 4)]
0.0000041626 [(2, 6, 5, 1)]
0.0000119403 [(3, 7, 5, 1)]
Converged. Norm of gradient: 2.482330523964407e-05
The final ansatz, optimized parameters and reference energies are available by print_summary
[6]:
ucc.print_summary()
################################ Ansatz ###############################
#qubits #params #excitations initial condition
8 9 14 RHF
############################### Energy ################################
energy (Hartree) error (mH) correlation energy (%)
HF -2.121387 46.173788 -0.000
MP2 -2.151794 15.766505 65.854
CCSD -2.167556 0.004979 99.989
UCC -2.167545 0.015250 99.967
FCI -2.167561 0.000000 100.000
############################# Excitations #############################
excitation configuration parameter initial guess
0 (2, 7, 5, 0) 10010110 -0.051907 -0.052049
1 (6, 3, 1, 4) 01101001 -0.051907 -0.052049
2 (2, 6, 5, 1) 01010101 -0.140231 -0.139297
3 (3, 7, 4, 0) 10101010 -0.033405 -0.033263
4 (6, 7, 5, 4) 11000011 -0.024488 -0.024327
5 (2, 3, 1, 0) 00111100 -0.024488 -0.024327
6 (3, 6, 5, 0) 01011010 -0.028461 -0.028758
7 (7, 2, 1, 4) 10100101 -0.028461 -0.028758
8 (2, 6, 4, 0) 01100110 -0.052825 -0.053072
9 (3, 7, 5, 1) 10011001 -0.030435 -0.030805
10 (6, 4) 01100011 -0.006359 -0.005294
11 (2, 0) 00110110 -0.006359 -0.005294
12 (7, 5) 10010011 0.004086 0.000000
13 (3, 1) 00111001 0.004086 0.000000
######################### Optimization Result #########################
e: -2.1675452943964704
fun: array(-2.16754529)
hess_inv: <9x9 LbfgsInvHessProduct with dtype=float64>
init_guess: [-0.052049049877468376, -0.13929721882902535, -0.033262956584275416, -0.02432719362945896, -0.02875765729787159, -0.05307218567505374, -0.030805233161950704, -0.005294244026331024, 0]
jac: array([ 5.07062545e-09, -8.83791785e-11, 1.30782196e-08, 1.70760122e-09,
4.83647155e-09, -3.33705792e-11, 3.54077142e-09, -1.48813139e-09,
-4.13038187e-09])
message: 'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
nfev: 13
nit: 11
njev: 13
opt_time: 0.014690637588500977
staging_time: 4.76837158203125e-07
status: 0
success: True
x: array([-0.0519072 , -0.14023057, -0.03340521, -0.02448758, -0.02846146,
-0.0528252 , -0.03043539, -0.00635861, 0.00408631])